Horner-Schema, Quotientenpolynome und VK-Zinsfaktoren eines Zahlungsstroms
⇒ Das Thema als PDF zum Download
Rudolf Pleier
Februar 2022
Die Beurteilung eines Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1}\) hinsichtlich seiner Vorteilhaftigkeit mit Hilfe der klassischen Methode des internen Zinssatzes (MIZ) verwendet einen festen, für alle Zinsperioden [k-1,k] (k = 1,…,n) der Laufzeit \(n \in \mathbb{N}\) konstanten und nicht (in Haben- und Sollzinsfaktor) gespaltenen Kalkulationszinsfaktor q = qK > 0 und einen ebenfalls auf die Zinsperioden bezogenen einzelnen internen Zinsfaktor q0 = qint(X) des Zahlungsstroms X. Als ein eingeschränkter Anwendungsbereich dieser MIZ wird in der Literatur gerne die Menge der Verrechnungskonto-Zahlungsströme (VK-Zahlungsströme, sog. isoliert durchführbare Zahlungsströme) X angegeben, die jeweils auf einem Konto mit qint(X) als Kontozinsfaktor verrechnet werden können, sodass die Kontostände Cj während der Laufzeit keinen Vorzeichenwechsel aufweisen und der Kontoendstand Cn gleich Null ist. Für diese VK-Zahlungsströme X ist die MIZ konsistent zur Kapitalwertmethode (KWM) und der jeweilige interne Zinsfaktor qint(X) auch noch ökonomisch interpretierbar als der Kontozinsfaktor eines Verrechnungskontos. Bei der näheren Untersuchung der VK-Zahlungsströme X bzw. der zugehörigen Endwertfunktionen En(X,q) trifft man auf die Begriffe Quotientenpolynome, Horner-Schema und Horner-Schema-Polynome, die hier nachfolgend und in der PDF-Datei eingehender behandelt werden. Insbesondere wird auch eine Aussage über die Vielfalt der Verrechnungskontozinsfaktoren (VK-Zinsfaktoren) eines Zahlungsstroms hergeleitet.
Zum Anwendungsbereich der MIZ mit der ihr eigenen Verwendung eines einzelnen internen Zinsfaktors ist anzumerken, dass dieser noch auf die Menge der NU- und NF-Zahlungsströme (Definition bei Pleier 2021, S. 293, 301) erweitert werden kann. Dabei wird bei der Begründung der MIZ für die NU-Zahlungsströme aber schon deutlich, dass hierbei tatsächlich die Vielfachheiten der internen Zinsfaktoren eine entscheidende Rolle spielen. Eine genauere Untersuchung dieses Gesichtspunkts führt dann zu einer auf ganz \(\mathbb{R}^{n+1}\) universell anwendbaren Verallgemeinerung der Methode, nämlich zur ‚Methode der Vielfachheiten der internen Zinsfaktoren (MVIZ)‘. Damit ist das Mysterium des eingeschränkten Anwendungsbereichs der Methode des internen Zinssatzes gelöst.
1 Horner-Schema und Quotientenpolynome
Ausgangspunkt der Betrachtungen ist ein Polynom Pn(q) n-ten Grades, das finanzmathematisch als Endwertfunktion En(q) =En(X,q) eines Zahlungsstroms X = (X0,X1,…,Xn)T \( \in \mathbb{R}^{n+1}\) (X0 ≠ 0) zum Kalkulationszinsfaktor q angesehen werden kann:
Pn(q) = En(q) = En(X,q) = X0qn + X1qn-1 +... + Xn-1q + Xn.
Der Polynomwert Pn(q) kann hinsichtlich des Rechenaufwands effizienter rekursiv mittels des sog. Horner-Schemas und der zugehörigen j-ten Horner-Schema-Polynomwerte Ej(q) berechnet werden:
E0(q) = X0,
Ej(q) = Ej-1(q)q + Xj (j = 1,…,n),
Pn(q) = En(q) = (…((X0q + X1)q + X2)q + …)q + Xn.
Die Horner-Schema-Polynome Ej(q) können dabei auch als die speziellen zur Stelle q0 = 0 gehörigen Quotientenpolynome des Polynoms Pn(q) angesehen werden: In absteigender Reihenfolge (j = n, n‑1, …, 1) ergibt sich nämlich das (j‑1)-te Horner-Schema-Polynom Ej‑1(q) als das zur Stelle q0 = 0 gehörige Quotientenpolynom des j‑ten Horner-Schema-Polynoms Ej(q). Mit Ej(0) = Xj gilt nämlich
\(E_{j-1}(q) = \dfrac {E_{j}(q)-X_{j}} {q} = \dfrac {E_{j}(q) - E_{j}(0)} {q - 0}\) (j = n,…,1; q ≠ 0).
Allgemeiner lassen sich zu einer beliebig vorgegebenen Stelle q0 \( \in \mathbb{R}\) ausgehend vom Polynom
Pn(q) = X0qn + X1qn-1 +...+ Xn (X0 ≠ 0)
und vom speziellen Polynomwert Pn(q0) in absteigender Reihenfolge für m = n, n‑1, …, 1 rekursiv die Quotientenpolynome
\(P_{m-1}(q) = P_{m-1}(q;q_0) \) = \(\dfrac {P_{m}(q) - P_{m}(q_0)} {q - q_0}\) = \(\sum_{j=0}^{m-1} a_j^{(m-1)}q^{m-1-j}\)
= \(a_0^{(m-1)}q^{m-1} + a_1^{(m-1)}q^{m-2} + ... + a_{m-1}^{(m-1)}\) (m = n,…,1; q ≠ q0)
vom Grad m‑1 bilden. Umgekehrt hat man bei bekanntem Quotientenpolynom Pm‑1(q) und Funktionswert Pm(q0) des Quotientenpolynoms Pm(q) (m = 0,…,n) an der Stelle q0 auch in aufsteigender Reihenfolge eine Rekursionsformel für das Quotientenpolynom Pm(q):
Pm(q) = (q - q0)Pm‑1(q) + Pm(q0) (m = 1,…,n).
Durch Koeffizientenvergleich dieser auf den beiden Seiten der Gleichung stehenden Polynome erhält man die folgende Rekursionsformel zur Berechnung der von der Stelle q0 abhängigen Koeffizienten \(a_j^{(m-1)} \) = \(a_j^{(m-1)}(q_0) \) des Quotientenpolynoms Pm‑1(q) = Pm‑1(q;q0) und des „Divisionsrestes“ Pm(q0) aus den Koeffizienten \(a_j^{(m)} \) des vorhergehenden Polynoms Pm(q) (m = n,...,1):
\(a_0^{(m-1)} = a_0^{(m)} (= \dots = a_0^{(n)} = X_{0} \neq 0)\),
\(a_j^{(m-1)} = q_0a_{j-1}^{(m-1)} + a_j^{(m)}\) (j = 1,…,m‑1),
\(a_m^{(m-1)} := P_m(q_0) = q_0a_{m-1}^{(m-1)} + a_m^{(m)}\).
In einer schematischen Darstellung dieser rekursiven Berechnung der Koeffizienten \(a_j^{(m-1)} \) von Pm‑1(q) erhält man das zum Polynom Pm(q) und zur Stelle q0 gehörige und in Abbildung 1 dargestellte einfache Horner-Schema, das zur Berechnung des Polynomwerts Pm(q0) über die Zwischenergebnisse \(a_j^{(m-1)} \) dient.

Abb. 1 Einfaches Horner-Schema für das Polynom Pm(q) und die Stelle q = q0 zur Berechnung des Polynomwerts Pm(q0) über die Zwischenergebnisse \(a_j^{(m-1)} \) (j = 0,...,m-1).
Speziell für m = n erfolgt mit dem Horner-Schema die Berechnung des Polynomwerts Pn(q0) des Ausgangspolynoms Pn(q) an der Stelle q0 über die Zwischenergebnisse \(a_j^{(n-1)} \) (j = 0,…,n‑1). Die Koeffizienten \(a_j^{(n-1)} \) des Quotientenpolynoms Pn‑1(q) berechnen sich dabei aus den Koeffizienten \(a_j^{(n)} \) = Xj des Ausgangspolynoms Pn(q) mit der Rekursionsformel
\(a_0^{(n-1)} = X_{0}, \)
\(a_j^{(n-1)} = q_0a_{j-1}^{(n-1)} + X_j\) (j = 1,…,n‑1),
\(a_n^{(n-1)} := P_n(q_0) = q_0a_{n-1}^{(n-1)} + X_n \),
welche mit der obigen Rekursionsformel der Horner-Schema-Polynomwerte Ej(q) an der Stelle q0 übereinstimmt. Demnach stimmen die Koeffizienten \(a_j^{(n-1)} = a_j^{(n-1)}(q_0) \) des Quotientenpolynoms Pn‑1(q) mit den speziellen Horner-Schema-Werten Ej(q0) überein:
\(a_j^{(n-1)} = E_j(q_0) \) für j = 0,…,n‑1,
\(P_n(q_0) = q_0a_{n-1}^{(n-1)} +X_n = E_n(q_0).\)
Eine Anwendung dieser Eigenschaft für den Index m = n erfolgt unten beim Beweis der Charakterisierung eines Verrechnungskontozinsfaktors (VK-Zinsfaktors) q0 von En(q), d. h. einer Stelle \(q_0 \in \mathbb{R}\) mit
En(q0) = 0, E(q0) = (E0(q0),…,En(q0))T \(\le\) O oder \(\ge\) O =(0,…,0)T,
durch das Auftreten von Quotientenpolynomkoeffizienten \(a_j^{(n-1)} \) ohne Vorzeichenwechsel. Als Folgerung erhält man hieraus noch die notwendige Nichtpositivität der weiteren reellen Nullstellen der Endwertfunktion En(q) neben einem VK-Zinsfaktor q0 von X bzw. En(q). Außerdem wird eine Aussage über die Vielfalt der VK-Zinsfaktoren gefolgert.
Die Nacheinanderberechnung der n Horner-Schemata für das Polynom Pn(q) zur Bestimmung der Koeffizienten der n Quotientenpolynome Pm-1(q) (m = n,…,1) zu einer fest vorgegebenen Stelle \(q_0 \in \mathbb{R}\) wird als vollständiges Horner-Schema bezeichnet. Dabei werden also der Reihe nach für m = n,…,1 die Koeffizienten \(a_j^{(m-1)} \) des Quotientenpolynoms Pm‑1(q) und der Polynomwert Pm(q0) berechnet. Nach n Schritten erhält man das konstante Polynom P0(q) \(\equiv \) \(a_0^{(0)} = X_0\) (\(\neq\) 0). In der Abbildung 2 ist eine komprimierte Darstellung des vollständigen Horner-Schemas angegeben, bei dem in der ersten Zeile die Koeffizienten Xj des Ausgangspolynoms Pn(q) = En(q) stehen und in den daruntergelegenen Zeilen jeweils die Koeffizienten \(a_j^{(m-1)} \) (j = 0,…,m‑1) des Quotientenpolynoms Pm‑1(q) und ganz rechts der Polynomwert Pm(q0) (m = n,…,1). In der ersten Zeile des komprimierten Schemas stehen also die Koeffizienten Xj des Ausgangspolynoms Pn(q) und in der ersten Koeffizientenspalte die Elemente \(a_0^{(m)} \) (m = n,…,0) mit dem Wert X0. Die übrigen Elemente \(a_j^{(m-1)} \) des komprimierten Schemas erhält man, indem man jeweils zum q0‑fachen des links davon stehenden Koeffizienten \(a_{j-1}^{(m-1)} \) den darüberstehenden Koeffizienten \(a_j^{(m)} \) addiert: \(a_j^{(m-1)} = q_0a_{j-1}^{(m-1)} + a_j^{(m)}\).
Das vollständige Horner-Schema liefert also auch die Polynomwerte Pm(q0) (m = n,…,0) der Quotientenpolynome Pm(q) an der Stelle q0 und damit damit auch die Koeffizienten bj der Entwicklung von Pn(q) an der Stelle q0, d. h. der Darstellung als Polynom in u = q - q0 (bj := Pj(q0)), und die Ableitungen \(P_n^{(n-j)}(q_0)\) der Polynomfunktion Pn(q) an der Stelle q0: \(P_n^{(n-j)}(q_0)\) = (n-j)!bj = (n-j)!Pj(q0). Der Beweis hierfür wird in der PDF-Datei gegeben.
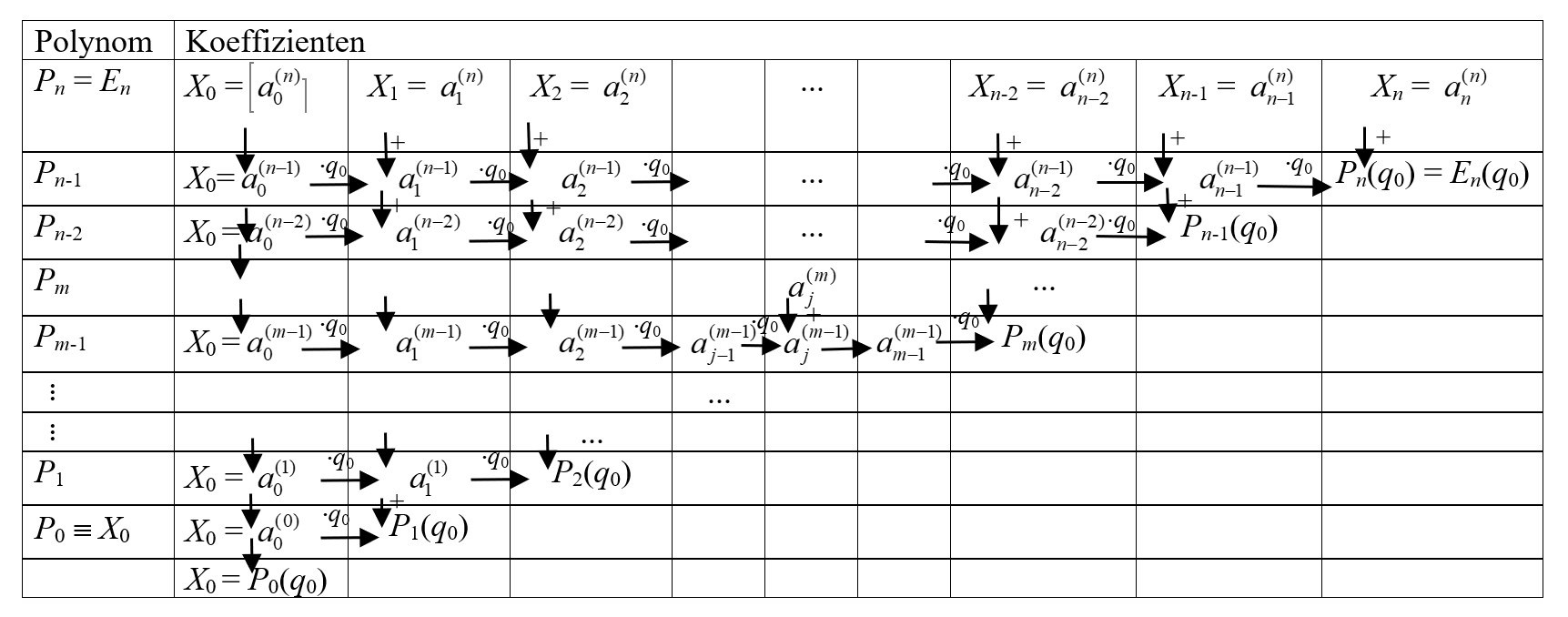
Abb. 2 Vollständiges Horner-Schema für das Polynom Pn(q) und die Stelle q = q0 zur Berechnung der Koeffizienten \(a_j^{(m)} \) der Quotientenpolynome Pm(q) (m = n-1,...,0) und der Polynomwerte Pm(q0) (m = n,...,0) in komprimierter Darstellung.
2 Entwicklung der Quotientenpolynome und deren k-ten Ableitungen an der Stelle q0
Durch die Ausführung der n Divisionsschritte erhält man eine Darstellung des Polynoms
Pn(q) = \(\sum_{j=0}^{n} b_j(q-q_0)^{n-j}\)
als Polynom in u = q - q0 mit den Koeffizienten
bj := Pj(q0) (j = 0,1,…,n).
Der Beweis erfolgt in der PDF-Datei mit der Rekursionsformel der Quotientenpolynome und dem Prinzip der vollständigen Induktion.
Die Funktionswerte Pm(q0) der Quotientenpolynome Pm(q) (m = 0,1,…,n) an der Stelle q = q0 stehen in enger Beziehung zu den Ableitungen des Ausgangspolynoms Pn(q) an dieser Stelle: Durch Koeffizientenvergleich der obigen Entwicklung von Pn(q) an der Stelle q0 mit der Taylorentwicklung
Pn(q) = \(\sum_{j=0}^{n} \frac{P_n^{(k)}(q_0)}{k!} (q-q_0)^{k}\)
der Funktion Pn(q) an der Stelle q0 erhält man nämlich für die k‑te Ableitung von Pn(q) an der Stelle q0 die Beziehung
\(P_n^{(k)}(q_0)\) = k!bn‑k = k!Pn‑k(q0) für k = 0,1,…,n,
\(P_n^{(k)}(q_0)\) = 0 für k > n.
Analog zum Ausgangspolynom Pn(q) erhält man auch für die Quotientenpolynome Pm(q) an der Stelle q0 die entsprechende Entwicklung
Pm(q) = \(\sum_{j=0}^{m} b_j(q-q_0)^{m-j}\) (m = 0,1,…,n)
und für deren k‑te Ableitung bei q0 die Beziehung:
\(P_m^{(k)}(q_0)\) = k!bm‑k = k!Pm‑k(q0) für k = 0,1,…,m; m = 0,…,n,
\(P_m^{(k)}(q_0)\) = 0 für k > m.
Durch k‑malige Differentiation der Entwicklung des Quotientenpolynoms Pm(q) an der Stelle q0 (als Polynom in u = q - q0) erhält man die entsprechende Entwicklung der k‑ten Ableitung \(P_m^{(k)}(q)\) des Quotientenpolynoms Pm(q):
\(P_m^{(k)}(q)\) = \(\sum_{j=0}^{m} (m-j) \dots (m-j-k+1)b_j(q-q_0)^{m-j}\) (u = q - q0, \(1 \le k \le m \le n\)).
3 Zwei Rekursionsformeln für die k-ten Ableitungen der Quotientenpolynome
Aus der Rekursionsformel der Quotientenpolynome Pm(q) erhält man auch zwei Rekursionsformeln für die k‑ten Ableitungen \(P_m^{(k)}(q)\) dieser Polynome:
\(P_m^{(k)}(q)\) = \(kP_{m-1}^{(k-1)}(q) + (q-q_0)P_{m-1}^{(k)}(q)\) (m = 1,…,n; k = 1,2,…),
\(P_m^{(k)}(q)\) = \(k \cdot\sum_{j=k-1}^{m-1} (q-q_0)^{j}P_j^{(k-1)}(q)\) (m = 1,…,n; k = 1,2,…).
Der Beweis erfolgt in der PDF-Datei mittels Differentiation und vollständiger Induktion. Dort werden auch zwei Rekursionsformeln für die k-ten Ableitungen der Horner-Schema-Polynome Em(q) bewiesen.
4 Charakterisierung eines Verrechnungskontozinsfaktors mittels Quotientenpolynomkoeffizienten ohne Vorzeichenwechsel
Bei der Beurteilung eines Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1}\) hinsichtlich seiner Vorteilhaftigkeit mittels der klassischen Methode des internen Zinssatzes (MIZ) wird in der Literatur als Anwendungsbereich der MIZ gerne die Menge der Verrechnungskonto-Zahlungsströme (VK-Zahlungsströme, sog. isoliert durchführbare Zahlungsströme) angegeben. Dies sind Zahlungsströme X = (X0,X1,…,Xn)T \(\in \mathbb{R}^{n+1}\) (X0 ≠ 0), die einen internen Zinsfaktor q0 = q0(X) \(\in \mathbb{R}\) besitzen, dessen Horner-Schema-Vektor E(q0) keinen Vorzeichenwechsel aufweist:
q0 \(\in \mathbb{R}\) mit En(q0) = 0 , E(q0) = (E0(q0),…, En(q0))T \(\le\) O oder \(\ge\) O.
Ein derartiger interner Zinsfaktor q0 wird hier als Verrechnungskontozinsfaktor (VK-Zinsfaktor) des Zahlungsstroms X bezeichnet. Im Falle einer Investition X (X0 < 0) wird q0 auch als Anlagezinsfaktor und im Falle einer Finanzierung X (X0 > 0) wird q0 auch als Darlehenszinsfaktor bezeichnet.
Im Falle eines positiven VK-Zinsfaktors q0 ist dieser die einzige positive Nullstelle, eine einfache Nullstelle und somit eine Vorzeichenwechselstelle der Endwertfunktion En(q). Im Falle eines nichtpositiven VK-Zinsfaktors q0 ist die Endwertfunktion En(q) auf der positiven Halbachse nullstellenfrei, sodass kein positiver interner Zinsfaktor existiert. Der Beweis dieser Aussagen erfolgt unten nach der Charakterisierung eines Verrechnungskontozinsfaktors. Auf diese VK-Zahlungsströme kann daher die MIZ mit der ihr eigenen Verwendung eines einzelnen internen Zinsfaktors problemlos in Konsistenz zur Kapitalwertmethode angewandt werden. Außerdem ist für diese Zahlungsströme noch die beliebte ökonomische Interpretierbarkeit des internen Zinsfaktors q0 als der Kontozinsfaktor qKto eines Verrechnungskontos gegeben, auf welches der Zahlungsstrom gebucht wird und dessen Kontostände Cj = Ej(q0) das Vorzeichen nicht wechseln. In der nachfolgenden Abbildung 3 erfolgt eine grafische Darstellung der Zahlungen Xj einer Finanzierung X = (X0,…,Xn)T (X0 > 0) und der nichtnegativen Horner-Schema-Werte Ej(q0) zu einem positiven Darlehenszinsfaktor q0.
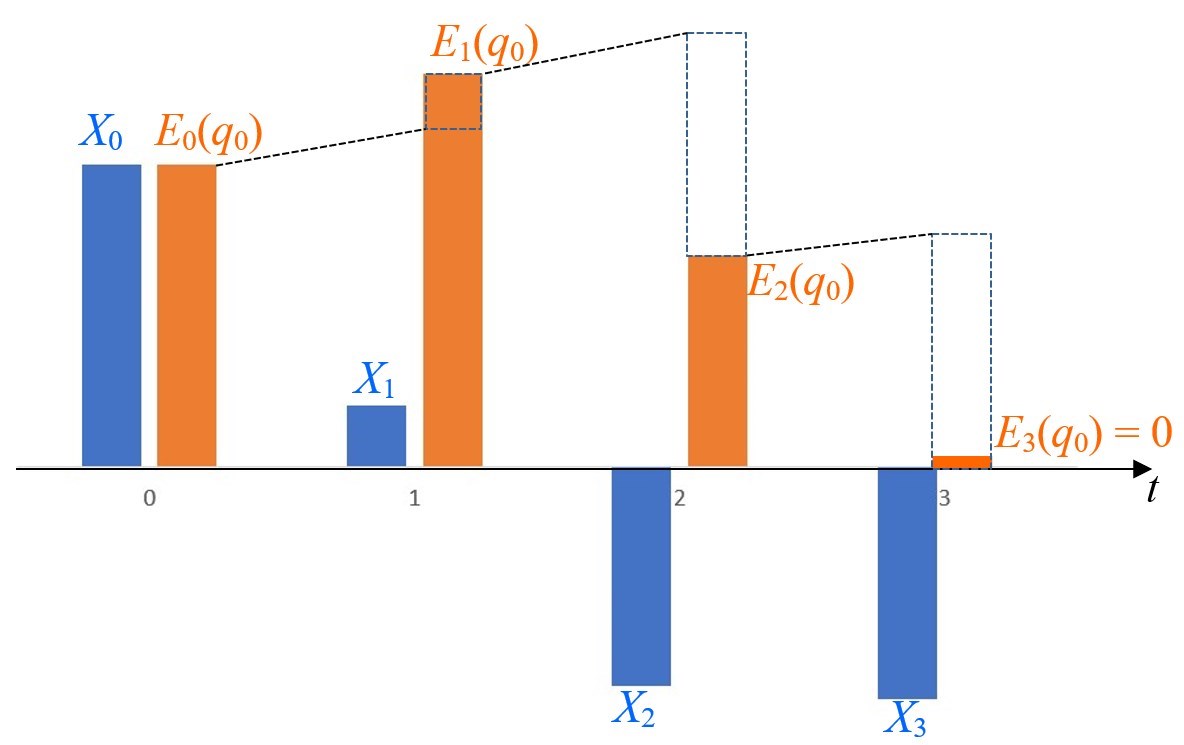
Abb. 3 Grafische Darstellung der Zahlungen Xj einer Finanzierung X = (X0,X1,X2,X3)T \(\in \mathbb{R}^4\) und der nichtnegativen Horner-Schema-Werte Ej(q0) zu einem positiven Darlehenszinsfaktor q0.
Eine funktionentheoretische Charakterisierung eines Verrechnungskontozinsfaktors q0 eines Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1}\) (X0 \(\neq\) 0) kann mittels der Koeffizienten des Quotientenpolynoms Pn-1(q) erfolgen:
Eine reelle Zahl q0 \(\in \mathbb{R}\) ist genau dann ein Verrechnungskontozinsfaktor des Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1} (X_0 \neq 0)\), d. h.
En(q0) = 0 , E(q0) \(\le\) O oder \(\ge\) O,
wenn die Koeffizienten aj (= \(a_j^{(n-1)} \) = Ej(q0)) des zur Stelle q0 und zur Endwertfunktion En(q) = Pn(q) gehörigen Quotientenpolynoms
Pn‑1(q) = \(\dfrac {E_{n}(q) - E_{n}(q_0)} {q - q_0}\) = \(\sum_{j=0}^{n-1} a_jq^{n-1-j}\)
keinen Vorzeichenwechsel haben:
a0 = X0 > 0, aj \(\ge\) 0 für j = 1,…,n‑1 oder
a0 = X0 < 0, aj \(\le\) 0 für j = 1,…,n‑1.
Der Beweis ergibt sich unmittelbar dadurch, dass die Koeffizienten aj des Quotientenpolynoms Pn‑1(q) der Endwertfunktion En(q) und der Stelle q0 mit den Horner-Schema-Werten Ej(q0) der Stelle q0 übereinstimmen (siehe Abschnitt 1).
Die funktionentheoretische Bedeutung der Existenz eines Verrechnungskontozinsfaktors q0 des Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1} (X_0 \neq 0)\) liegt demnach in der Möglichkeit einer Produktdarstellung der Endwertfunktion
En(q) = En(q) - En(q0) = (q - q0)Pn‑1(q)
mit dem Linearfaktor q - q0 und einem Polynom Pn‑1(q) vom Grad n‑1, dessen Koeffizient a0 zur höchsten Potenz qn‑1 von Null verschieden ist und dessen weitere Koeffizienten a1, …, an‑1 im Falle a0 > 0 alle nichtnegativ und im Falle a0 < 0 alle nichtpositiv sind. Das Quotientenpolynom Pn‑1(q) zu einem beliebigen Verrechnungskontozinsfaktor q0 ist also stets nullstellenfrei auf \(]0,\infty[\): Beispielsweise gilt im Falle a0 = X0 > 0 die Abschätzung
Pn‑1(q) ≥ a0qn-1 > 0 für q > 0.
Aus der Produktdarstellung En(q) = (q - q0)Pn‑1(q) folgt außerdem die folgende Aussage über die Nullstellenverteilung von En(q) auf der positiven Halbachse:
Nullstellenverteilung der Endwertfunktion En(X,q) auf der positiven Halbachse \(]0,\infty[\) für einen VK-Zahlungsstrom X:
Im Falle eines positiven VK-Zinsfaktors q0 des Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1} (X_0 \neq 0)\) ist die Stelle q0 eine einfache Nullstelle und die einzige positive Nullstelle von En(q).
Im Falle eines nichtpositiven VK-Zinsfaktors q0 ist En(q) nullstellenfrei auf der positiven Halbachse \(]0,\infty[\).
Bei Existenz eines positiven VK-Zinsfaktors gibt es insbesondere keinen weiteren positiven VK-Zinsfaktor und bei Existenz eines nichtpositiven VK-Zinsfaktors gibt es gar keinen positiven VK-Zinsfaktor. Aufgrund dieser zweiten Aussage gibt es bei Existenz eines positiven VK-Zinsfaktors dann auch noch keinen nichtpositiven VK-Zinsfaktor. Insgesamt erhält man die folgende Aussage zur Vielfalt der VK-Zinsfaktoren:
Vielfalt der VK-Zinsfaktoren eines Zahlungsstroms:
Ein positiver VK-Zinsfaktor q0 des Zahlungsstroms \(\mathbf{X} \in \mathbb{R}^{n+1} (X_0 \neq 0)\) ist stets auf ganz \(\mathbb{R}\) der einzige VK-Zinsfaktor von X.
Neben einem nichtpositiven VK-Zinsfaktor q0 gibt es keinen positiven VK-Zinsfaktor, also höchstens noch nichtpositive VK-Zinsfaktoren. Die Anzahl K der nichtpositiven VK-Zinsfaktoren kann dabei im Allgemeinen die Werte 1, 2, …, n-2, n annehmen.
Diese letzte Aussage über die mögliche Anzahl der nichtpositiven VK-Zinsfaktoren eines Zahlungsstroms wird bewiesen im Thema ‚Verrechnungskontozinsfaktoren eines Zahlungsstroms‘.
Aus der obigen Charakterisierung eines Verrechnungskontozinsfaktors ergeben sich auch noch weitere Folgerungen, insbesondere noch unter der zusätzlichen Voraussetzung eines nichtnegativen oder positiven Verrechnungskontozinsfaktors. Die Aussagen werden nachfolgend o. E. nur für einen nichtnegativen oder positiven Darlehenszinsfaktor formuliert, da sie analog auch für einen nichtnegativen oder positiven Anlagezinsfaktor gelten.
5 Positivität aller Quotientenpolynome Pm(q) und der zugehörigen k-ten Ableitungen auf der positiven Halbachse für einen nichtnegativen Darlehenszinsfaktor q0
Für einen nichtnegativen Darlehenszinsfaktor q0 einer Finanzierung X (X0 > 0; En(q0) = 0, E(q0) \(\ge\) O) gelten für die Quotientenpolynome Pm(q) (m = 1,…n‑1) und deren k‑ten Ableitungen \(P_m^{(k)}(q)\) bis zur Ordnung k = m auf der positiven Halbachse \(]0,\infty[\) folgende Abschätzungen:
P0(q) \(\equiv\) \(a_0^{(0)}\) = X0 > 0 (m = 0),
Pm(q) = \(\sum_{j=0}^{m} a_j^{(m)}q^{m-j}\) \(\ge\) \(a_0^{(m)}q^m\) > 0 für q > 0 (m = 1,…n‑1),
\(P_m^{(k)}(q)\) = \(\sum_{j=0}^{m-k} (m-j) \dots (m-j-k+1)a_j^{(m)}(q-q_0)^{m-j-k}\)
\(\ge\) \(m\dots (m-k+1)a_0^{(m)}q^{m-k}\) > 0 für q > 0 (\(1 \le k \le m \le n-1\)).
Der Beweis dieser Aussagen wird in der PDF-Datei angegeben. Dort wird auch noch die Positivität der Horner-Schema-Polynome Em(q) und der k-ten Ableitungen \(E_m^{(k)}(q)\) im Intervall q > q0 für einen positiven Darlehenszinsfaktor q0 bewiesen.
In der Abbildung 4 sind zum positiven Darlehenszinsfaktor q0 = 1,10 der bereits für die Abbildung 3 verwendeten Finanzierung X = (X0,X1,X2,X3)T = (100;20;-73;-77)T die Endwertfunktion E3(q) und die auf der positiven Halbachse \(]0,\infty[\) positiven Quotientenpolynome Pj(q) (j = 0, 1, 2) dargestellt.
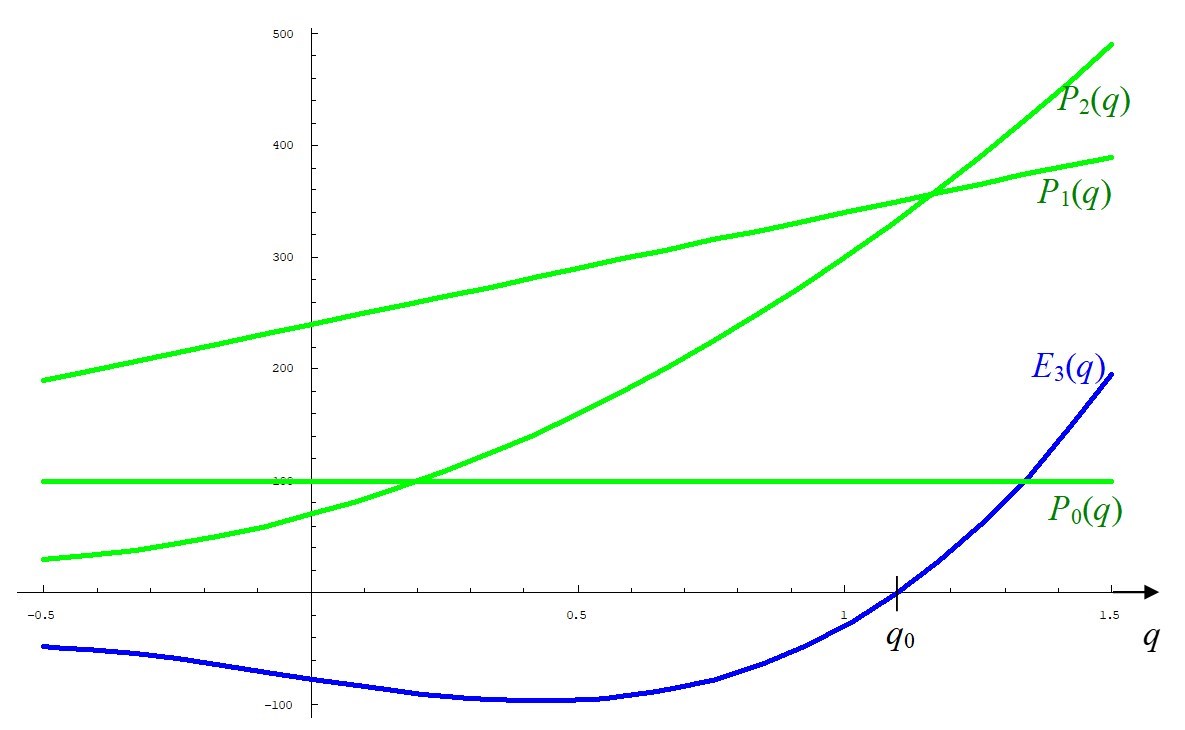
Abb. 4 Grafische Darstellung der Endwertfunktion E3(q) und der auf \(]0,\infty[\) positiven Quotientenpolynome Pj(q) für eine Finanzierung X \(\in \mathbb{R}^4\) mit einem positiven Darlehenszinsfaktor q0.