Die SE-Halbordnung
⇒ Das Thema als PDF zum Download
Rudolf Pleier
Juni 2015
Bei der Beschreibung eines Anwendungsbereichs der Methode des internen Zinssatzes für die Beurteilung eines einzelnen Zahlungsstroms \(\mathbf{X} = (X_0,...,X_n)^\text{T} \in \mathbb{R}^{n+1} \) bzw. für den Vergleich alternativer Zahlungsströme X, Y \( \in \mathbb{R}^{n+1} \) wird auch die Konsistenz dieser Beurteilung bzw. dieses Vergleichs mit der sogenannten SE-Halbordnung betrachtet. Diese SE-Halbordnung wird als Durchschnittsrelation \(\succcurlyeq_\varLambda\) aller Endwert-Präferenzordnungen (E-Präferenzordnungen) \(\succcurlyeq_{\text{E},q}\), q > 0, gebildet. Sie wird daher im Folgenden als die (für alle Kalkulationszinsfaktoren q) simultane Endwert-Halbordnung (SE-Halbordnung) bezeichnet:
\(\varLambda \: := \: \succcurlyeq_\varLambda \: := \: \underset{q > 0}\bigcap \succcurlyeq_{\text{E},q}\)
\(\mathbf{X} \succcurlyeq_\varLambda \mathbf{Y} \::\Leftrightarrow \: \mathbf{X} \succcurlyeq_{\text{E},q}\mathbf{Y} \text{ für alle } q > 0\)
\(\Leftrightarrow \: E_n(\mathbf{X},q) \ge E_n(\mathbf{Y},q) \text{ für alle } q > 0\).
In der PDF-Datei wird bewiesen, dass diese Durchschnittsrelation eine Halbordnung des Vektorraums \(\mathbb{R}^{n+1} \) ist mit den fünf Eigenschaften der Reflexivität, Transitivität, Identitivität und Abgeschlossenheit bezüglich der nichtnegativen Skalarmultiplikation und bezüglich der Addition.
Weiter wird gezeigt, dass die SE-Halbordnung \(\varLambda\) konvex, monoton und eine Erweiterung der natürlichen Halbordnung \(\ge\) ist, für \(n=1\) beide Halbordnungen übereinstimmen und für \(n\ge 2\) die natürliche Halbordnung eine echte Teilmenge der SE-Halbordnung ist.
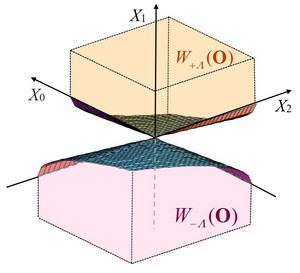
Abb. 1 Der \(\varLambda\)-nichtnegative Kegel \(W_{+ \varLambda}(\mathbf{O})\) und der \(\varLambda\)-nichtpositive Kegel \(W_{\text{-} \varLambda}(\mathbf{O})\) = \(\text{-} \: W_{+ \varLambda}(\mathbf{O})\) der SE-Halbordnung \(\varLambda\) für die Laufzeit n = 2