Dr. Dr. Rudolf Pleier

Willkommen auf der Autoren-Website
von Dr. Dr. Rudolf Pleier
 

Der Autor

Dr. Dr. Rudolf Pleier ist 1948 in Etzenricht in der Oberpfalz (Bayern) geboren. In den 1970er Jahren studierte er Mathematik und Physik an der Universität Würzburg mit den Abschlüssen Diplom und Promotion. Bei seiner Existenzgründung wurden ihm verschiedene Finanzierungen angeboten, von denen er mit einer geeigneten Methode die für ihn optimale auswählen wollte. Inspiriert durch dieses Schlüsselerlebnis befasst er sich seit vielen Jahren mit der Finanzmathematik und insbesondere mit der Bewertung von Zahlungsströmen.
 

Etzenricht im Naturpark Nördlicher Oberpfälzer Wald

Die Bücher

Finanzmathematik - Bewertung von Zahlungsströmen

Das Buch gibt eine leicht verständliche Einführung in die Bewertung sicherer diskreter Zahlungsströme. Es wendet sich an Studierende der Finanz- und Wirtschaftsmathematik im Grundstudium und ist zum Selbststudium geeignet.

Mittels einfacher Beispiele (Robinson beim Fischfang und Robinson auf dem Kartoffelmarkt) werden zunächst möglichst allgemeine Definitionen der Konzepte der Nachbildung (additiven Zerlegung, Duplizierung) und der Glattstellung (additiven Ergänzung, Replizierung) für die Beurteilung und den Vergleich von sicheren Zahlungsströmen X = (X₀,X₁,…,X_n) ∈ ℝⁿ⁺¹ bei unvollkommenem Kapitalmarkt in der Vektorschreibweise entwickelt. Verwendet werden dazu eine streng monoton steigende und an den Intervallgrenzen unbeschränkte Beurteilungskurve (Bewertungskurve, Zielsetzungskurve, Präferenzkurve) W(μ) im ℝⁿ⁺¹ und ein Supplementsystem L, d. h. ein Satz aus n linear unabhängigen Investitionen und n linear unabhängigen Finanzierungen, für die Bildung der Ergänzungsgeschäfte (Supplemente). Die verschiedenen Ansätze der Literatur von Fisher (1932) über Heister (1962) und Kruschwitz (1978) bis Grob (1999) ergeben sich als Spezialfälle. Für die mit den beiden Konzepten konstruierten Präferenzordnungen ⊵_D,L,W und ⊵_R,L,W werden die Eigenschaften und die Vielfalt beschrieben.

Die klassischen mit einem konstanten Kalkulationszinssatz definierten Methoden (Endwert-, Kapitalwert-, Zeitwert- und Annuitätenmethode) bei vollkommenem Kapitalmarkt und bestimmte Verallgemeine­rungen dieser Methoden bei unvollkommenem Kapitalmarkt werden als spezielle Replizierungsmethoden jeweils mit spezieller Beurteilungskurve und speziellem Supplementsystem eingeordnet. Damit können auch deren implizite Prämissen hinsichtlich der real benötigten Supplementmenge auf dem Kapitalmarkt exakt angegeben werden. Weiter kann die Übereinstimmung von Zeitwert-Präferenzordnungen, die zu verschiedenen Vergleichszeitpunkten gehören, wie beispielsweise von Barwert- und Endwert-Präferenzordnung, durch Bedingungen an die allgemeineren Transpositionsfaktoren charakterisiert werden.    

Für die vieldiskutierte klassische Methode des internen Zinssatzes wird das Mysterium ihres eingeschränkten Anwendungsbereichs aufgeklärt und eine universell einsetzbare Verallgemeinerung sowohl für die Beurteilung als auch für den Vergleich bereitgestellt. Mit einfacher Oberstufenmathematik, nämlich der Kurvendiskussion der Kapitalwertfunktion (Barwertfunktion) B_n(X,q) als Funktion des Zinsfaktors q, kann die Beurteilung eines Zahlungsstroms X ∈ ℝⁿ⁺¹ nach der Kapitalwertmethode (Barwertmethode) bzw. das Vorzeichen des Kapitalwerts (Barwerts) B_n(X,q_K) zum Kalkulationszinsfaktor q = q_K im Fall B_n(X,q_K) ≠ 0 charakterisiert werden durch die Ungerad- bzw. Geradzahligkeit der Nullstellenanzahl rechts des Kalkulationszinsfaktors q_K. Hinsichtlich einer Verallgemeinerung der Methode mit nicht eingeschränktem Anwendungsbereich ist also der Blick von einer einzigen irgendwie festgelegten Nullstelle q_int zu lösen und auf die Gesamtheit der Nullstellen q_j rechts von q_K zu richten. Der Vergleich zweier Zahlungsströme X, Y ∈ ℝⁿ⁺¹ erfolgt durch die Beurteilung des Differenzzahlungsstroms D = X - Y. Diese verallgemeinerte Methode der Vielfachheiten der internen Zinsfaktoren ist dann äquivalent zu den anderen klassischen Methoden und löst das Rätsel der traditionell mit einem einzigen internen Zinssatz angewandten Methode.   

Blick ins Buch bei: Amazon
Weitere Infos: hier
Buch als PDF: Finanzmathematik

Diskrete stochastische Finanzmathematik

Das Buch gibt eine leicht verständliche Einführung in die zeit­diskrete stochas­ti­sche Finanzmathematik. Es wendet sich an Studierende der Finanz- und Wirt­­schaftsmathematik im Grundstudium und ist zum Selbst­studium ge­eig­net.

Die Bewertung zustandsabhängiger Zahlungsprofile erfolgt mit einem Markt­mo­dell bei vollkommenem Kapi­talmarkt nach dem Duplikationsprinzip. Die Behand­­lung des Mehrperiodenmodells kann dabei ohne Rückführung auf die ent­­haltenen Einperiodenmodelle dargestellt werden. Das Einperioden­modell ergibt sich zwar als Spezialfall des Mehrperiodenmodells, wird aber dennoch auch noch ausführ­lich in seiner in der Literatur üblichen speziellen Schreib­­­­weise in den niedrigerdi­mensionalen Räumen beschrieben. Außer­dem er­folgt eine geson­derte Betrach­tung für den Spezialfall der endfälligen Zah­lun­gen, die mit sog. selbstfinanzieren­den Handelsstrategien dupliziert werden.   

Es werden für das Mehrperiodenmodell, das Einperioden­modell und das Modell endfälliger Zahlungen etliche neue Charakteri­sierungen der zent­ralen Begriffe Law of One Price, Vollständigkeit und Arbitragefreiheit herge­lei­tet. Die Charakterisierungen erfolgen nicht nur durch Preisgleichungen, sondern auch durch Lagebe­ziehungen von bestimmten Unter­­räumen und des nichtnegati­ven Orthanten und können damit auch geometrisch vi­sua­li­siert wer­den. Es werden die mathematischen Strukturen aufgezeigt, die den Marktmodellen beim Vorliegen dieser besonderen Eigenschaften zugrundeliegen.

Im Mehrperiodenmodell zu den N ausgewählten und modellierten Finanzinstrumenten S^j und deren natürliche Filtration ℱ von \(\sigma\)-Algebren wird für den Raum 𝒲 der ℱ-adaptierten reellwertigen Zahlungsprofile X und den Raum ℋ_N der ℱ-vorhersehbaren ℝ^N-wertigen Handelsstrategien h jeweils ein geeignetes Skalarprodukt bereitgestellt. Die lineare Abbildung L : ℋ_N → 𝒲, die jeder Handelsstrategie h die Portfolioauszahlung X = L(h) zuordnet, wird beschrieben durch eine Darstellungsmatrix in Form einer oberen Blockbidiagonalmatrix, deren Blöcke wiederum Blockdiagonalmatrizen sind. Es existiert dann die zur linearen Abbildung L eindeutig bestimmte adjungierte Abbildung L* : 𝒲 → ℋ_N, die als Darstellungsmatrix die Transponierte L^T der Darstellungsmatrix von L besitzt. Für die Berechnung einer Duplikationsstrategie h eines Zahlungsprofils X wird durch Nutzung der speziellen Matrixstruktur ein hinsichtlich des Zeitparameters t und hinsichtlich der Partitionsmenge A_t‑1,k ∈ 𝒫_t-1 gestaffeltes lineares Gleichungssystem angegeben. Es wird die Äquivalenz der Vollständigkeit (VS) des Mehrperiodenmodells zur Vollständigkeit aller enthaltenen Einperiodenmodelle begründet. Der Nachweis eines Bewertungsprozesses Ψ mit den Preisgleichungen für die Berechnung der Preise der duplizierbaren Zahlungsprofile bei gültigem Law of One Price (LOP) erfolgt auf drei verschiedenen Wegen, nämlich 1) mittels spezieller Unterraumstrukturen (𝒱  ∩ ℳ = O, ℳ^⊥ = ker L* ⨁ lin Ψ, b = L*(Ψ) ∈ L*(𝒲)), 2) mit dem Rieszschen Darstellungssatz und 3) mit einem Alternativsatz der konvexen Geometrie. Dieser Alternativsatz liefert auch die Existenz eines Diskontierungsprozesses Φ bei Arbitragefreiheit (AF), die Existenz eines positiven Normalenvektors Q_T zum Unterraum ℳ_T der NE-Zahlungs­profile bei sf-Arbitragefreiheit (AFsf) und eine geometrische Interpretation des schrittweisen Übergangs vom LOP zur Arbitragefreiheit. Für die Berechnung eines Bewertungsprozesses Ψ wird ein gestaffeltes lineares Gleichungssystem angegeben. Es wird der Zusammenhang zwischen dem LOP im Mehrperiodenmodell und dem LOP in den enthaltenen Einperiodenmodellen untersucht und eine hinreichende Bedingung für deren Äquivalenz angegeben (Ψ_t(A_t,k) ≠ 0 ∀ t ∈ {0,…,T-1} und A_t,k ∈ 𝒫_t). Weiter wird die Äquivalenz der Arbitragefreiheit (AF) des Mehrperiodenmodells zur Arbitragefreiheit der enthaltenen Einperiodenmodelle bewiesen. Für die vielzitier­ten Begriffe formale Maße und formale W-Maße, stochas­ti­scher Diskon­tie­rungsfaktor, Arrow-Debreu-Preis, Zu­standspreis und Er­eig­nis­preis, Dis­kont­vektor, Arrow-Debreu-Preis­­­vektor, Zu­stands­preis­vektor und Ereignis­preis­vektor, Diskontie­rungs­­vek­­­tor, Diskontierungsprozess, Zu­stands­preisprozess, deter­ministischer Diskon­tie­­­rungsfaktor, deterministischer Dis­kontierungs­vektor, de­ter­ministi­scher Preis­vek­­tor, formale oder syntheti­sche Preis­­maße und einheitliches Preis­­­maß, Martin­gal­maß und risikolo­ses bzw. risiko­neu­tra­les Wahr­scheinlich­keits­­maß wer­den die jeweiligen impliziten Voraussetzungen plausibel dargestellt: Ar­bitra­ge­­frei­heit, Duplizier­bar­keit bestimm­ter Arrow-Debreu-Pa­piere, Voll­stän­dig­keit des Marktmodells und Exis­tenz soge­nann­ter fest­­verzins­licher Han­dels­­strategien. Für die Bewertung der stochastischen Zahlungsprofile nach dem Duplikationsprinzip werden verschiedene Interpretationen angegeben und damit auch Brücken von der Bewertung deterministischer Zahlungsströme zur Bewertung stochastischer Zahlungsströme geschlagen. Es sind dies die Interpretation als Abstandsmessung zur Hyperebene der Kapitalmarktgeschäfte, als Beurteilung nach dem Duplizierungskonzept mit der Beurteilungskurve der Sofortentnahme und einem Ergänzungsgeschäft vom Kapitalmarkt und als Barwertberechnung auf drei Arten der Diskontierung.   

Im Mehrperiodenmodell der endfälligen Zahlun­gen wird der erste und zweite Hauptsatz der Preistheorie verallgemeinert. Statt dividendenloser Marktmodelle werden jetzt auch dividendenversehene Marktmodelle zugelassen. Die sf-Arbitragefreiheit (AFsf) (d. h. das Fehlen von selbstfinanzierenden Arbitragegelegenheiten) wird nun charakterisiert durch die Existenz von mindestens einem positiven Normalen­vektor Q zum Unterraum ℳ_T der NE-Zahlungs­profile (der sf-duplizierbaren Zahlungsprofile mit dem Startkapitaleinsatz bzw. Preis Null). Die sf-Vollständigkeit (VSsf) eines sf-arbitragefreien Marktmodells wird charakterisiert durch die Existenz von genau einem derartigen positiven Normalenvektor Q zu ℳ_T. Im Spezialfall eines dividendenlosen Marktmodells mit Numéraire wird die sf-Arbitragefreiheit (AFsf) charakterisiert durch die Existenz von einem o. E. auf die Komponentensumme κ(Q) = 1_Ω^TQ = 1 normierten positiven Normalenvektor  zum Unter­raum   im relati­ven Marktmodell bzw. durch die Existenz von einem sog. äquivalenten Martingalmaß. Die Charakterisierung der sf-Arbit­rage­freiheit und der sf-Vollständig­keit erfolgt also sowohl linearalgebraisch mit­tels eines positiven Normalenvektors als auch wahr­schein­lich­­­keits­­the­oretisch mittels eines äquivalenten Mar­tingalmaßes. Ein κ-normierter positiver Normalenvektor ist im relativen Marktmodell (mit seinem konstanten Numéraire 1) stets ein Diskontvektor (positiver Bewertungsvektor), mit dem der Preis eines duplizierbaren Zahlungsprofils berechnet werden kann. Im ursprünglichen Marktmodell gilt dies jedoch nur unter zusätzlichen Voraussetzungen. Für ein Marktmodell mit Numéraire wird die Äquivalenz der sf-Arbitragefreiheit im Mehrperiodenmodell zur sf-Arbitragefreiheit in allen enthaltenen Einperiodenmodellen gezeigt (Einperiodenarbitrage, lokale Arbitrage; Beweis im relativen Marktmodell). Weiter wird der Zusammenhang zwischen der sf-Vollständigkeit (VSsf) im Mehrperiodenmodell und der Vollständigkeit in den enthaltenen Einperiodenmodellen untersucht und eine hinreichende Bedingung für deren Äquivalenz angegeben (S_t(A_t,k) ≠ 0 ∀ t ∈ {0,…,T-1}, A_t,k ∈ 𝒫_t, LOP gültig in den enthaltenen Einperiodenmodellen). Der Nachweis eines Bewertungsvektors Ψ_T mit seinen Preisgleichungen für die Berechnung der Preise der sf-duplizierbaren endfälligen Zahlungsprofile X_T bei gültigem Law of One Price erfolgt auf drei verschiedenen Wegen, nämlich 1) mittels spezieller Unterraumstrukturen (𝒱₀ ∩ ℳ_T = O, ℳ_T^⊥ =  ⨁ lin Ψ_T), 2) mit dem Rieszschen Darstellungssatz und 3) durch Herleitung aus einem Bewertungsprozess Ψ mit seinen Preisgleichungen in L(ℋ_N) des allgemeinen Mehrperiodenmodells.             

Im Spezialfall des Einperiodenmodells (T = 1) wird die Äquivalenz der verschiedenen Begriffe der Duplizierbarkeit und die Äquivalenz der verschiedenen Begriffe der Vollständigkeit begründet. Wie schon im Mehrperiodenmodell der endfälligen Zahlungsprofile gezeigt wird, sind auch im Einperiodenmodell verschiedene Begriffe des LOP äquivalent. Weiter ist im Einperiodenmodell das LOP äquivalent zur Existenz eines Bewertungsprozesses Ψ = (Ψ₀,Ψ₁)^T und äquivalent zur Existenz eines Bewertungsvektors Ψ₁. Außerdem ist die allgemeine Arbitragefreiheit (AF) äquivalent zur Existenz eines Diskontierungsprozesses (positiven Bewertungsprozesses) Φ = (Φ₀,Φ₁)^T und äquivalent zur Existenz eines Diskontvektors (positiven Bewertungsvektors) Φ₁. Die speziellere sf-Arbitragefreiheit (AFsf) ist dagegen nur äquivalent zur Existenz eines positiven Normalenvektors Q₁ zum Unterraum ℳ₁ der NE-Zahlungsprofile. Wie allgemeiner im Mehrperiodenmodell der endfälligen Zahlungsprofile liefert auch im Einperiodenmodell der positive ℳ₁-Normalenvektor Q₁ erst unter zusätzlichen Voraussetzungen und nach der κ-Normierung auf die Komponentensumme κ(Q₁) = κ₀ = π(1_Ω) (> 0) einen Diskontvektor Φ₁ für die Bewertung der Zahlungsprofile X₁ ∈ ℝ^Ω. Speziell im Einperiodenmodell folgt dann aber auch die Existenz eines Diskontierungsprozesses Φ für die Bewertung der Zahlungsprofile (X₀,X₁) ∈ ℝ^1+K und die allgemeine Arbitragefreiheit (AF). Es wird eine hinreichende Bedingung (GI) angegeben, unter der im Einperiodenmodell die spezielle sf-Arbitragefreiheit (AFsf) äquivalent zur allgemeinen Arbitragefreiheit (AF) ist. Außerdem werden einige in der Literatur vielzitierte Begriffe wie formales W-Maß, Preismaß, Martingalmaß und risikoneutrales W-Maß im Einperiodenmodell erläutert.     

Reinlesen bei: Tredition
Blick ins Buch: Amazon
Ausgewählte Themen: hier
Buch als PDF: Diskrete stoch. Finanzmath.

Nullstellenverteilung der Lösungen

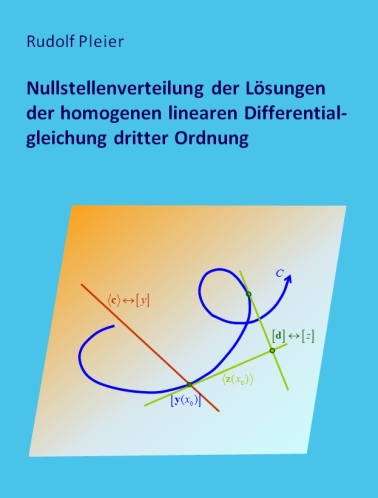In der vorliegenden Arbeit werden im ersten Kapitel Methoden entwickelt, mit denen Bedingungen an die komplexwertigen Koeffizienten der linearen Differentialgleichung dritter Ordnung gewonnen werden können, die hinreichend für das Nichtauftreten gewisser Nullstellenkonfigurationen bei den Lösungen und deren Ableitungen sind.

Im zweiten Kapitel wird für reellwertige Koeffizienten das Raumpaar aus den Lösungsräumen der Differentialgleichung (L) und der dazu adjungierten Differentialgleichung (L⁺) mit einem skalaren Produkt B ausgestattet und damit ein duales Raumpaar erhalten. Es können allgemeine Wechselbeziehungen zwischen den Nullstellenverteilungen der Lösungen von (L) und (L⁺) hergeleitet werden hinsichtlich Oszillation, Existenz von nichtoszillatorischen, schwach oszillatorischen und stark oszillatorischen zweidimensionalen Unterräumen, Charakterisierungen von speziellen Doppelkegelstrukturen der Menge der nichtoszillatorischen Lösungen durch asymptotische Eigenschaften der Lösungen, Diskonjugiertheit an den Intervallgrenzen und der lokalen Diskonjugiertheit. Außerdem werden anstelle der Verwendung spezieller Koeffizientenbedingungen nun Klassen von Differentialgleichungen durch den Ausschluss gewisser Nullstellenkonfigurationen bei bestimmten Standardlösungen definiert und Wechselbeziehungen zwischen den Klassen von (L) und (L⁺) dargestellt.

Im dritten Kapitel wird die schon 1905 von Wilczynski und 1911 von Birkhoff verwendete Integralkurve C in der projektiven Ebene dargestellt, die man erhält, wenn man die Funktionswerte eines beliebig fixierten Fundamentalsystems von (L) als die homogenen Koordinaten eines Punktes in der projektiven Ebene interpretiert. Damit können die Nullstellen einer Lösung von (L) durch die Treffpunkte einer Geraden mit der Integralkurve und die Nullstellen einer Lösung von (L⁺) durch die Tangenten eines Punktes an die Integralkurve veranschaulicht werden. Allgemeiner wird gezeigt, dass eine bestimmte Gerade durch einen bestimmten Punkt genau dann geht, wenn die zugehörigen Lösungen von (L) und (L⁺) bezüglich des skalaren Produkts B orthogonal sind. Es werden verschiedene Klassen der Differentialgleichungen mittels der besonderen Gestalt der Integralkurve C veranschaulicht und umgekehrt geometrische Eigenschaften von C mittels spezieller Lösungen analytisch charakterisiert. In Verallgemeinerung eines von Birkhoff geometrisch begründeten Trennungssatzes für die Nullstellen von Lösungen werden weitere Sätze über die Nullstellenanzahl von orthogonalen bzw. nicht orthogonalen Lösungen analytisch bewiesen.

Im vierten Kapitel werden Eigenschaften der Klassen K_I und K_II aufgezeigt hinsichtlich Charakterisierungen der Diskonjugiertheit, Charakterisierung der nichtoszillatorischen Lösungen als die nullstellenfreien Lösungen, Existenz von nichtnegativen nichttrivialen Lösungen, Existenz von stark oszillatorischen zweidimensionalen Unterräumen, Oszillation von (L) und (L⁺), Diskonjugiertheit an den Intervallgrenzen und Existenz von nullstellenfreien Lösungen. Ferner wird die von Birkhoff geometrisch begründete Charakterisierung der Klasse K_I ∪ K_II, bei der die Tangenten von C das vorhergehende bzw. das nachfolgende Kurvenstück nicht schneiden, durch die nach außen bzw. innen verlaufende Spiralform der Integralkurve C hier analytisch bewiesen. In diesem Zusammenhang werden auch Hilfspunkte als Endpunkte maximaler Intervalle einer bestimmten Klassenzugehörigkeit definiert, einige Hilfssätze bereitgestellt und insbesondere neue Erkenntnisse über die Differenzierbarkeit der durch die ersten konjugierten Punkte gegebenen Funktion η hergeleitet.

Buch bei: Amazon
Leseprobe bei: Westarp
Weitere Info: hier
Buch als PDF: Nullstellenverteilung der Lösungen