Charakterisierung der Kapitalwertmethode mittels interner Zinsfaktoren
⇒ Das Thema als PDF zum Download
Rudolf Pleier
November 2021
Die klassische Kapitalwertmethode (Barwertmethode, B-Beurteilung und B-Vergleich, Abk. KWM, BWM) vergleicht und beurteilt Zahlungsströme \(\mathbf{X}, \mathbf{Y} \in \mathbb{R}^{n+1}\) nach der Vorgabe eines für alle Zinsperioden [k-1,k] (im Allgemeinen Jahre; k = 1,…,n) der Laufzeit \(n \in \mathbb{N}\) konstanten und nicht (in Haben- und Sollzinsfaktor) gespaltenen Kalkulationszinsfaktors q = qK = 1 + iK \(\in\) ]0,∞[ (iK \(\in\) ]-1,∞[ Kalkulationszinssatz) mit der klassischen Kapitalwertfunktion (Barwertfunktion)
Bn(X) = Bn(X,q) = X0 + X1q-1 + ... + Xnq-n
= En(X,q)/qn
als Nutzenfunktion:
\(\mathbf{X} \succcurlyeq_\text{B} \mathbf{Y}\) (X ist mindestens so vorteilhaft wie Y)
\(:\iff\) Bn(X) ≥ Bn(Y);
\(\mathbf{X} \succ_\text{B} \mathbf{O}\) (X ist vorteilhaft bzw. vorteilhafter als O = (0,…,0)T)
\(:\iff\)Bn(X) > Bn(O) = 0.
Äquivalenz der klassischen Methoden: Da die klassischen Nutzenfunktionen zum Vergleich von Zahlungsströmen, nämlich die Endwertfunktion En(X), die Barwertfunktion (Kapitalwertfunktion) Bn(X), die Zeitwertfunktion Zm,n(X) (zum Vergleichszeitpunkt m) und die Annuitätenfunktion \(\alpha_n(\mathbf{X})\), sich untereinander jeweils nur durch einen positiven konstanten Faktor unterscheiden,
Bn(X) = En(X)/qn,
Zm,n(X) = En(X)/qm-n,
\(\alpha_n(\mathbf{X})\) = En(X)/En(A) (\(\mathbf{A} \underset{\cdot}{>} 0\), d. h. \(\mathbf{A} \ge 0 \: \land \: \mathbf{A} \neq 0 \)),
liefern sie dieselbe Präferenzordnung (Pleier, 2021, S. 209)
\(\succcurlyeq_\text{E}\) = \(\succcurlyeq_\text{B}\) = \(\succcurlyeq_\text{Z}\) = \(\succcurlyeq_\text{A}\).
Demzufolge ist die nachfolgende Charakterisierung der Endwertmethode auch eine Charakterisierung der anderen klassischen Methoden, nämlich der Barwertmethode (Kapitalwertmethode), Zeitwertmethode und Annuitätenmethode. Sie liefert aber nur auf einem eingeschränkten Anwendungsbereich eine Charakterisierung der traditionellen Methode des internen Zinssatzes, die nur einen einzigen internen Zinssatz des Zahlungsstroms verwendet.
B-Beurteilung: Die B-Beurteilung bzw. gleichbedeutend dazu die E-Beurteilung eines Zahlungsstroms \(\mathbf{X} = (X_0,...,X_n)^\top \in \mathbb{R}^{n+1}\) lässt sich mittels der internen Zinsfaktoren qj dieses Zahlungsstroms bzw. der reellen Nullstellen qj der zugehörigen Endwertfunktion \(q \mapsto E_n(\mathbf{X},q)\) charakterisieren. Dazu verwendet man bei fest gedachtem Koeffizienten-(n+1)-Tupel X die Anzahl \(U_{>q_K}\) der reellen Nullstellen der Polynomfunktion \(q \mapsto E_n(\mathbf{X},q)\) von jeweils ungerader Vielfachheit im offenen Intervall \(]q_K,\infty[\) bzw. die
Gesamtordnung \(m_{>q_K}\) der Nullstellen von \(E_n(\mathbf{X},q)\) in \(]q_K,\infty[\)
und bestimmt deren Parität (Ungerad- bzw. Geradzahligkeit). Ein Beweis für die Charakterisierung und eine ausführlichere Darstellung des Themas wird in der PDF-Datei angegeben. Der Beweis verwendet die Produktdarstellung der Polynomfunktion \(q \mapsto E_n(\mathbf{X},q)\) mittels ihrer reellen Nullstellen qj und ihrer Vielfachheiten mj und eine einfache Kurvendiskussion. Damit wird die Endwertmethode bzw. die Kapitalwertmethode charakterisiert durch die Parität (Ungerad- bzw. Geradzahligkeit) der Gesamtordnung \(m_{>q_K}\) der internen Zinsfaktoren qj von X rechts des Kalkulationszinsfaktors qK. Beispielsweise ist eine Investition \(\mathbf{X} \in \mathbb{R}^{n+1}\) genau dann vorteilhaft mit positivem Kapitalwert Bn(X,qK), wenn diese Gesamtordnung ungerade ist. Die Investition ist genau dann unvorteilhaft mit negativem Kapitalwert Bn(X,qK), wenn diese Gesamtordnung gerade ist.
Für eine Investition (einen lexikonegativen Zahlungsstrom) \(\mathbf{X} \in \mathbb{R}^{n+1}\) erhält man die folgende Charakterisierung der B-Beurteilung:
\(\mathbf{X} \sim_\text{B} \mathbf{O}\) (X ist B-indifferent)
⟺ qK ist ein interner Zinsfaktor von X;
\(\mathbf{X} \succ_\text{B} \mathbf{O}\) (X ist (echt) B-vorteilhaft)
⟺ qK ist kein interner Zinsfaktor von X ∧ \(m_{>q_K}\) ungerade;
\(\mathbf{X} \prec_\text{B} \mathbf{O}\) (X ist (echt) B-unvorteilhaft)
⟺ qK ist kein interner Zinsfaktor von X ∧ \(m_{>q_K}\) gerade.
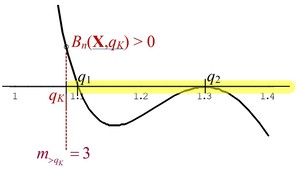
Abb. 1 Der Graph der Kapitalwertfunktion (Barwertfunktion) \(q \mapsto B_n(\mathbf{X},q)\) einer für den Kalkulationszinsfaktor qK B-vorteilhaften Investition X mit ungerader rechtsseitiger Gesamtvielfachheit \(m_{>q_K}\) der internen Zinsfaktoren
Die Charakterisierung der B-Beurteilung einer Finanzierung (eines lexikopositiven Zahlungsstroms) \(\mathbf{X} \in \mathbb{R}^{n+1}\) erhält man, indem man in der obigen Charakterisierung die Eigenschaften ‚ungerade‘ und ‚gerade‘ vertauscht.
B-Vergleich: Aufgrund der Linearität der Kapitalwertfunktion Bn(X,q) bezüglich des Koeffizienten-(n+1)-Tupels X erhält man daraus unmittelbar auch eine Charakterisierung des B-Vergleichs von Zahlungsströmen. Die Charakterisierung des B-Vergleichs für Zahlungsströme \(\mathbf{X}, \mathbf{Y} \in \mathbb{R}^{n+1}\), deren Differenzzahlungsstrom D = X - Y o. E. eine Investition ist, lautet folgendermaßen:
\(\mathbf{X} \sim_\text{B} \mathbf{Y}\) \(\iff\) qK ist ein interner Zinsfaktor von D;
\(\mathbf{X} \succ_\text{B} \mathbf{Y}\) \(\iff\) qK ist kein interner Zinsfaktor von D \(\land\) \(m_{>q_K}(\mathbf{D})\) ungerade;
\(\mathbf{X} \prec_\text{B} \mathbf{Y}\) \(\iff\) qK ist kein interner Zinsfaktor von D \(\land\) \(m_{>q_K}(\mathbf{D})\) gerade.
Universelle Methode mit internen Zinsfaktoren: Mit dieser Charakterisierung der Kapitalwertmethode erhält man sowohl für die Beurteilung als auch für den Vergleich von Zahlungsströmen eine Methode der Vielfachheiten der internen Zinsfaktoren (MVIZ), die universell auf ganz \( \mathbb{R}^{n+1}\) bzw. auf ganz \( \mathbb{R}^{n+1} \times \mathbb{R}^{n+1}\) definiert und äquivalent ist zur Endwertmethode, zur Barwertmethode (Kapitalwertmethode), zur Zeitwertmethode und zur Annuitätenmethode. Im Gegensatz zur bisher üblichen Methode des internen Zinssatzes (MIZ), die nur einen einzigen irgendwie ausgewählten internen Zinssatz verwendet, fällt bei der MVIZ die Einschränkung auf einen begrenzten Anwendungsbereich weg. Die MVIZ ist die Verallgemeinerung einer jeden irgendwie definierten MIZ mit einem einzelnen internen Zinsfaktor. Damit ist auch das Mysterium der Einschränkung des Anwendungsbereichs (des Bereichs der Konsistenz zur KWM) der traditionellen MIZ aufgeklärt.
Rechenaufwand und Kondition der MVIZ: Für die praktische Anwendung der MIZ und der MVIZ ist zu beachten, dass bei der im Allgemeinen nötigen iterativen Bestimmung der Nullstellen qj des Polynoms En(X,r) ein viel höherer Aufwand anfällt als bei der Berechnung des einzigen Funktionswerts Bn(X,qK) bei der KWM. Außerdem ist die Nullstellenbestimmung für ein Polynom En(X,r) = X0rn + … + Xn in der Standarddarstellung mit den Koeffizienten Xj (j = 0,…,n) schlecht konditioniert. Dabei können schon einfache Nullstellen schlecht konditioniert sein, während mehrfache Nullstellen stets schlecht konditioniert sind. Dies heißt, dass ein kleiner relativer Fehler in den als Ausgangsdaten vorgegebenen Koeffizienten Xj große relative Fehler in den Rechenresultaten für die Polynomnullstellen qj bewirkt. Bei einer speziellen Wahl des Kalkulationszinsfaktors qK kann dies dann auch zu einer anderen Gesamtvielfachheit \(m_{>q_K}\) der reellen Polynomnullstellen qj im Intervall \(] q_K,\infty[\) und zu einer anderen Beurteilung von X führen. Ein Zahlenbeispiel für den Fall, dass eine geringe relative Änderung einer Zahlungsstromkomponente schon eine Änderung der Beurteilung des Zahlungsstroms verursachen kann, wird in der PDF-Datei gegeben.